“Good! He did not have enough imagination to become a mathematician.”
— Hilbert's response upon hearing that one of his students had dropped out to study poetry.
(wiki)
Do you love mathematics as much as we do? Over the years, we’ve developed five constraint solvers and a lot of other software that’s mathematically sophisticated, and through that we have gained some understanding in this area of expertise.
So, today we want to talk about the seemingly impossible: things that you can understand but also seem like just a fantasy. Yes, right now! The beauty of mathematics is that there really are a lot of remarkable sides to it that everyone can enjoy.
For example, can you imagine a thing with a surface area of zero but with sides that are infinitely long? Or can you imagine an object with a dimension greater than 1 but fewer than 2?
People say that mathematics is always like that: either it’s not clear as to how it works, or that it isn’t clear what its purpose is. But today we're going to look at some examples that have concrete benefits, are clear – and just plain wonderful looking!
Definitions
Reading definitions that are boring is typically not a very interesting exercise. Here’s one: “In mathematics, a fractal is a subset of Euclidean space with a fractal dimension that strictly exceeds its topological dimension” (wiki).
So instead, let’s draw a fractal to make the definition obvious: the fractal known as the Sierpiński carpet.
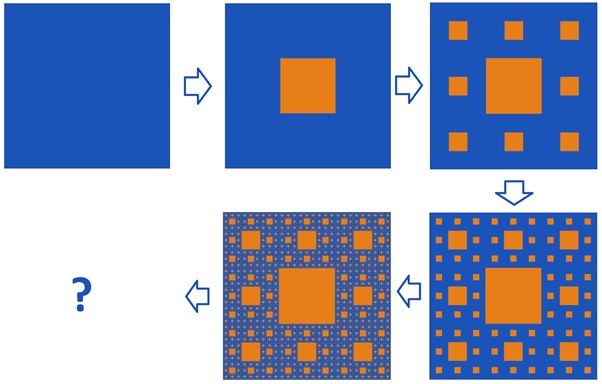
It was described 105 years ago by Wacław Sierpiński. The idea is simple: at each step, split a blue square into a 3x3 grid, and then change the color of the central square to orange. If we do this operation an infinite number of times, we end up with a very special blue surface that has a dimension of (log 8)/(log 3) ≈ 1.8928 (more than 1, fewer than 2), with an area of zero and sides that are infinitely long – just as I had promised.
OK, so it looks nice, but who would want such a thing? You would! It turns out that you use it every day that you access a Wi-Fi device: it employs a fractal-shaped antenna. So, it is not only about our imaginations; it proves to be useful, as well.
Generating Fractals of Your Own
Now that you understand how fractals work, you can create something that looks nice! How hard do you think it is to draw this picture?

It turns out it is really quite simple to draw, if you use a special language for this. The fractal description here is very short:
{"depth":9,"n":2,"rules":[[100,1,0,0],[1,1,1,1]],"colors":["#1a54b9","#e77e18"]}
You can access the code and the rules here.
When you make just a little change to the program, like this
{"depth":9,"n":2,"rules":[[200,1,0,0],[1,1,1,1]],"colors":["#1a54b9","#e77e18"]}
you generate a fractal that looks very different, like this one:

The second fractal description is listed here.
LEDAS Fractal Language
These instructions are very short, but very powerful. You don't even need to understand this language, let’s call it Ledas Fractal Language, because we’ve implemented it for you as a visual editor. With this editor you can set the
- number of colors
- size of the grid
- depth (number of iterations)
- rules.
The rules are simple: you can get a feel for how easy the rules are when you begin to start playing with fractals. Let’s look at the rules that generate the Sierpiński carpet:
{"depth":5,"n":3,"rules":[[0,0,0,0,1,0,0,0,0],[1,1,1,1,1,1,1,1,1]],"colors":["#1a54b9","#e77e18"]}
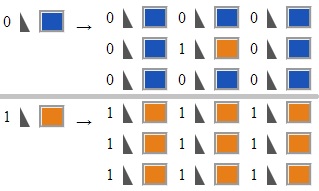
What we see in the illustration above are the following rules:
- Each blue square is to be replaced by eight blue squares and an orange one at the center
- Each orange square is to be replaced with nine orange squares.
- The black triangles indicate that no cells are to be rotated or mirrored.
You can play with it in our simulator here.
History and Acknowledgements
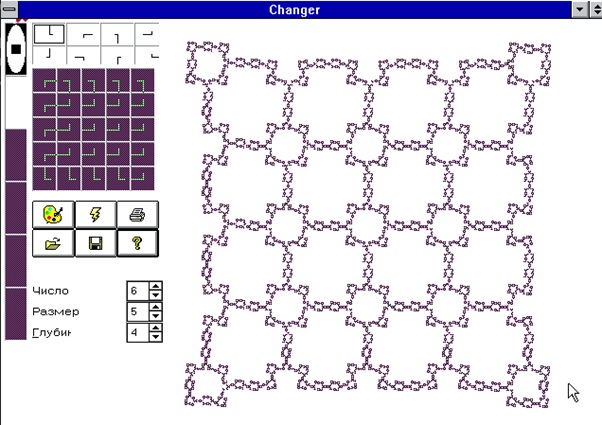
The idea for our Ledas Fractal Language came from the program Changer2 (© 1997 Yuri Khan, license CC0 v.1.0 or later), which is based on Changer.exe. We could not track down the original, but some sources claim that Evgeny Kashmensky implemented that first program. The Changer2 program was implemented more than two decades ago, so it is not easy to run it on today’s computers; you would need an old version of Windows for it.
Changer2 looks like this, along with a nice-looking fractal:
The LEDAS Fractal Contest
We are happy that a simple description for fractals exists and that everyone can invent and draw nice-looking patterns with our new generator. Now we call on you to draw fractals of your own.
We invite readers to send us programs written in LEDAS Fractal Language that draw new fractals. You can use more colors and bigger grids to generate fractals that look really nice. Also, we can recommend playing this generator with children, because they have super imaginations.
Send your fractals to quiz@ledas.com. Anna, the designer of all of our isicad magazine covers, will choose the best images.
We will post the names and generated fractals of all who submit it. (If you don't want your name posted, then please say so in your submission.) We look forward to seeing what you come up with!